Computational Mechanics
Our team has a strong background in computational mechanics and steadily develops, applies, and improves numerical techniques for the solution of problems in the mechanics and physics of materials and structures. We are particularly interested in providing state-of-the-art tools for our own research, e.g., to support the scale-bridging investigation of advanced materials (such as ferroelectric ceramics or magnesium alloys) or to investigate extreme scenarios where classical computational methods fail (e.g., the large deformation and distortion of rubbery materials or cellular metamaterials by meshfree techniques).
Computational mechanics has evolved tremendously over the past decades, turning techniques such as finite element analysis (FEA) and computational fluid dynamics (CFD) at the larger scales, phase field modeling at the mescoale, as well as molecular dynamics (MD) and density functional theory (DFT) into versatile numerical tools. In addition, all of those are nowadays readily available in both commercial and open-source format, so they enjoy world-wide popularity across science and engineering (not confined to mechanics but also becoming state of the art in related disciplines such as e.g. physics, chemistry, biology, medicine, etc.).
All models are wrong but some are useful. George E.P. Box
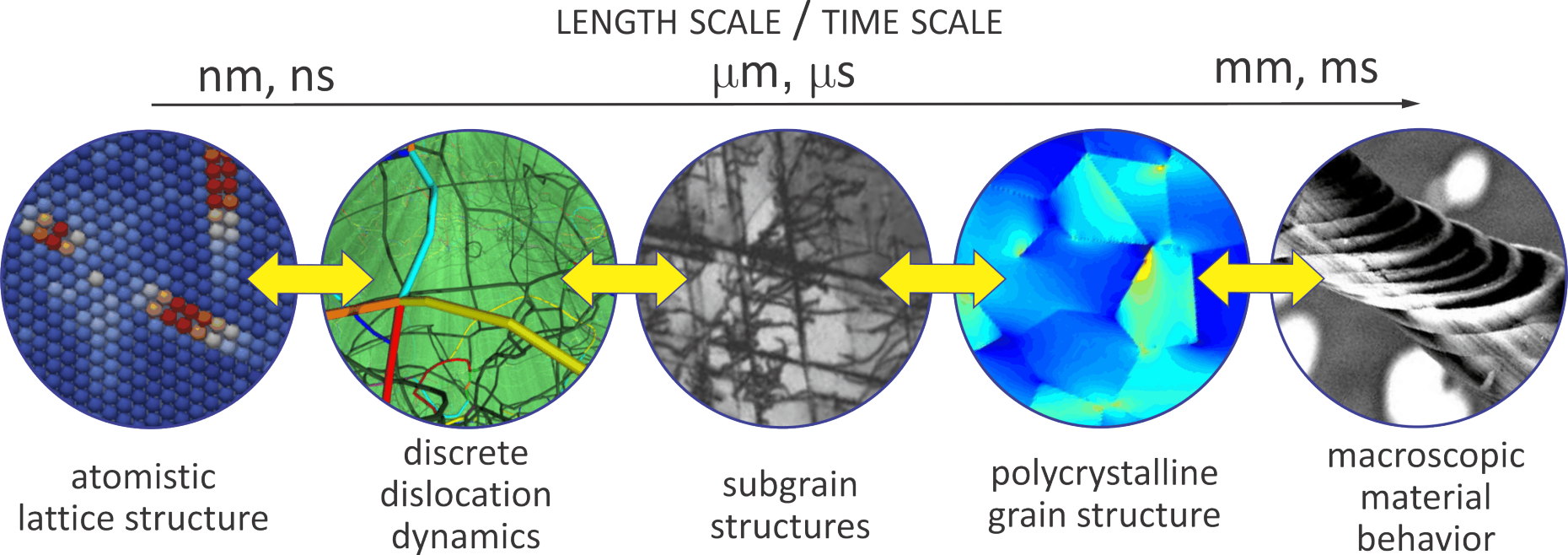
Our main motivation are the limitations of those techniques presently available. Whenever material behavior requires novel, extraordinary or complex simulation techniques, existing methods may reach their limits. This is true e.g. for scale-bridging phenomena that extend across many length and time scales. Consider e.g. microstructural processes in materials (such as diffusion or defect interactions) that require atomistic resolution for an accurate description but extend by orders of magnitude beyond the length and time scale confinements inherent in atomistic methods such as MD. Or consider mesoscale models of e.g. metal plasticity or phase transformation and separation in solids, where extremely high resolution is required for models to accurately represent physical reality, but where most standard techniques (and especially commercial codes) face strong limitations. Of, finally, consider problems involving extreme deformation such as the deformation of rubbery or tissue materials (stretchable by many hundreds of percent strain) or metal forming (involving not only very large strains but also significant local distortion and material rearrangement besides complicated material-level phenomena). Such problems, which we face in our research, are difficult to simulate using existing techniques. This is why we develop and apply new tools to meet our demands.
For example, we develop methods of coarse-grained atomistics which bridge across length and time scales, enabling the simulation of processes with atomic-level resolution by significantly larger specimen dimensions and/or time scales of interest. We further work on Fast Fourier Transform (FFT)-based solvers which render 3D high-resolution simulations at the mescoale feasible on laptops or small servers. Of course, we also exploit high-performance computing to arrive at scalable codes that exploit ETH Zürich's resources such as Euler. We also develop meshless modeling methods such as enhanced maximum-entropy schemes, which bypass the need for a finite element mesh and are excellently suited for problems involving extreme deformation and/or distortion.
Codes
We generally strive for open-source codes to be released for general use by the scientific community. Some have been released already, others are still in the development and testing phases. If you are interested in using some of our codes, please follow this link
Education
Our interest in computational mechanics (among others) also influences our teaching. With many commercial and open-source tools available for computer simulations, what becomes more essential than ever is a solid education and training of our next-generation scienstists and engineers to use those tools and to understand their concepts (rather than producing colorful pictures with minimal background knowledge and little reliability or accountability of the produced simulation outcome). To this end (and together with the Institute of Mechanical Systems), we offer courses ranging from Introduction to Finite Elements to Multiscale Modeling.
See our Education overview