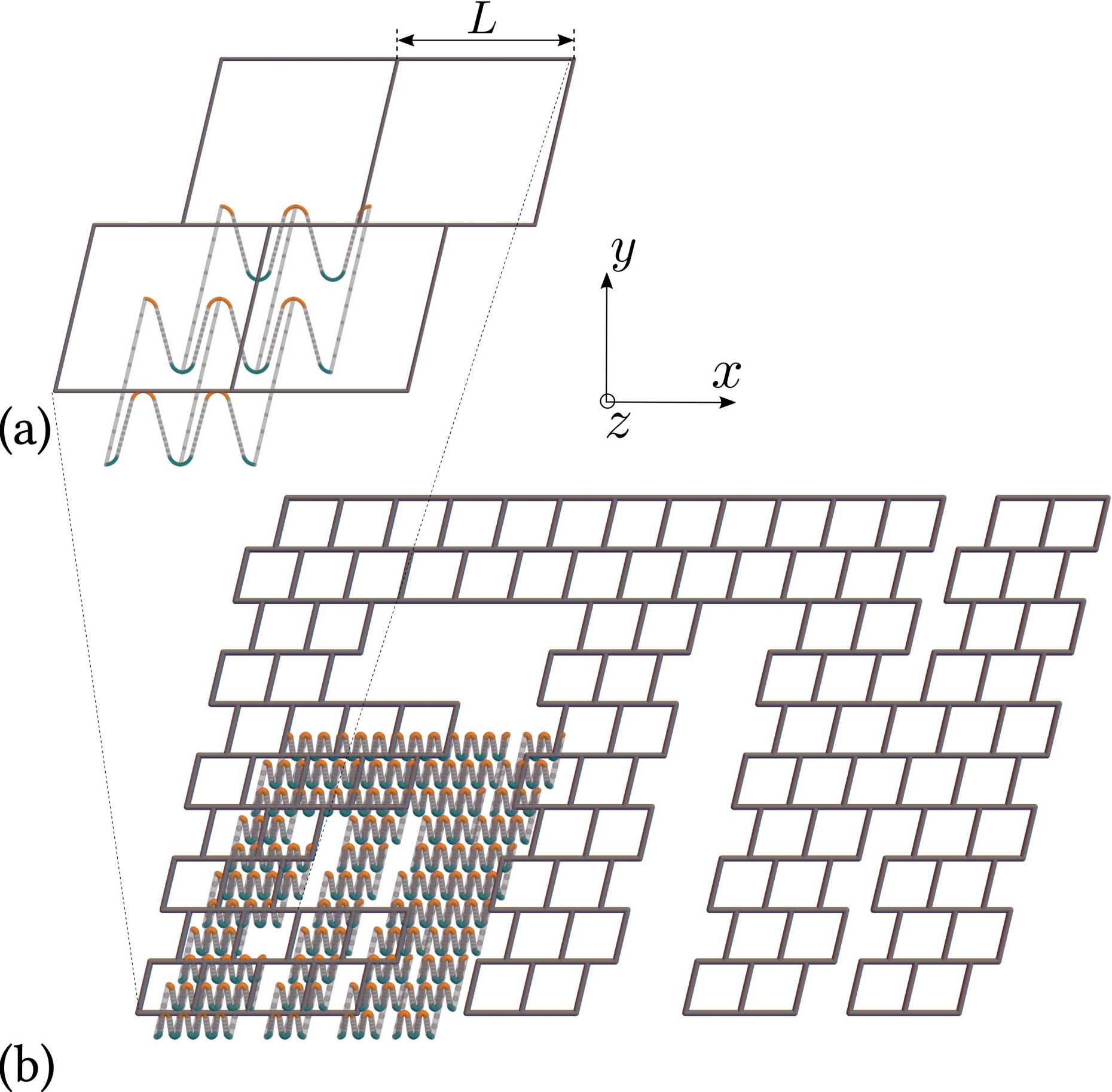
Discrete Beams
Additive manufacturing technologies offer new opportunities in terms of material design and complexity of shapes and structures. Networks of flexible, slender structural elements, which may incorporate so-called active materials, e.g. shape memory polymers, photo-elastic materials and swelling composites, are the current state of the art. Understanding and tailoring these new (meta-)materials, as well as predicting their mechanical response in an efficient and accurate manner remains a challenge. Capturing the mechanical response of truss networks includes both complex constitutive behaviours, for example hyper-viscoelastic materials, and intricate geometries including heterogeneous cross-sections and complex network arrangements. We have developed a discrete, geometrically exact description of flexible beam networks and morphing structures at finite strains.
We have introduced a geometrically exact, discrete beam formulation based on the differential geometry of framed curves in a time-discrete setting for time and history-dependent constitutive models, adapted from a formulation originating from the computer graphics community. In contrast to previous formulations, we separate the beam kinematics from the constitutive law of the underlying material. This modular approach allows for an implementation of a wide variety of constitutive laws, such as e.g. elastic, inelatistic, viscous- and hyperelastic materials. Further, our approach describes beam bending without the introduction of rotational degrees of freedom but through the kinetic extraction of an effective beam curvature from the positions of the vertices of a discrete framed curve. To accommodate rigid junctions required for the computation of beam networks, we introduced a new technique based on a virtual (ghost) segment on which a rigid rotational constrain is imposed. Our nonlinear discrete beam code, the UtoBeams library developed in C++, is available external page here.
We demonstrated the versatility and efficiency of our 1D model with a suite of examples. Fig. 1 shows a programmable elastomeric structure. Upon thermal activation, the initially straight structure (without natural curvature) shrinks into the coloured version, where the green segments possess a positive natural curvature, while the orange segments have a negative natural curvature.
Depicted in Fig. 2 are our simulation results of a so-called pop-up structure (demonstrated experimentally by Yan et al (2016)), inspired by the novel manufacturing and deployment technique for 3D structures, which exploits the self-assembly (the pop-up) of initially flat, multi-layered thin structures made of slender ribbons, attached to a pre-strained substrate. Under an equibiaxial compression, the assembly buckles due to the prestreched substrate. We demonstrate the efficiency and validity of our numerical framework compared to expensive shell computations. See Lestringant and Kochmann (2020) for more details.
Current research aims at extending the model to finite deformations. We follow a formal asymptotic dimension reduction approach that starts from a nonlinear 2D or 3D model, as proposed by Lestringant and Audoly (2020). We implement a systematic numerical method to arrive at an accurate and efficient 1D model of hyperelastic slender solids at finite strains, capturing a variety of cross-sectional geometries, as well as constitutive behaviours, which is ultimately implemented in our nonlinear discrete beam numerical framework.
Code
Our discrete beam implementation is available as an open-source C++ library. Find out more