Multiscale Modeling
Multiscale modeling techniques are powerful tools to bridge across multiple scales, aimed at linking macroscopic behavior to microscale features and mechanisms. How e.g. do the mechanical properties of engineering materials emerge from the complex interplay of atoms, crystal defects and grain boundaries? How do composites derive their beneficial properties? Why do man-made metamaterials excell exceptional properties? In this course, we discuss the theoretical foundations and numerical applications of multiscale modeling in solid mechanics, from electronic-structure and atomistic techniques all the way up to the macroscopic continuum scale with a focus on scale-bridging methodologies (including atomistics, meoscale models, computational homogenization, and multiscale constitutive modeling).
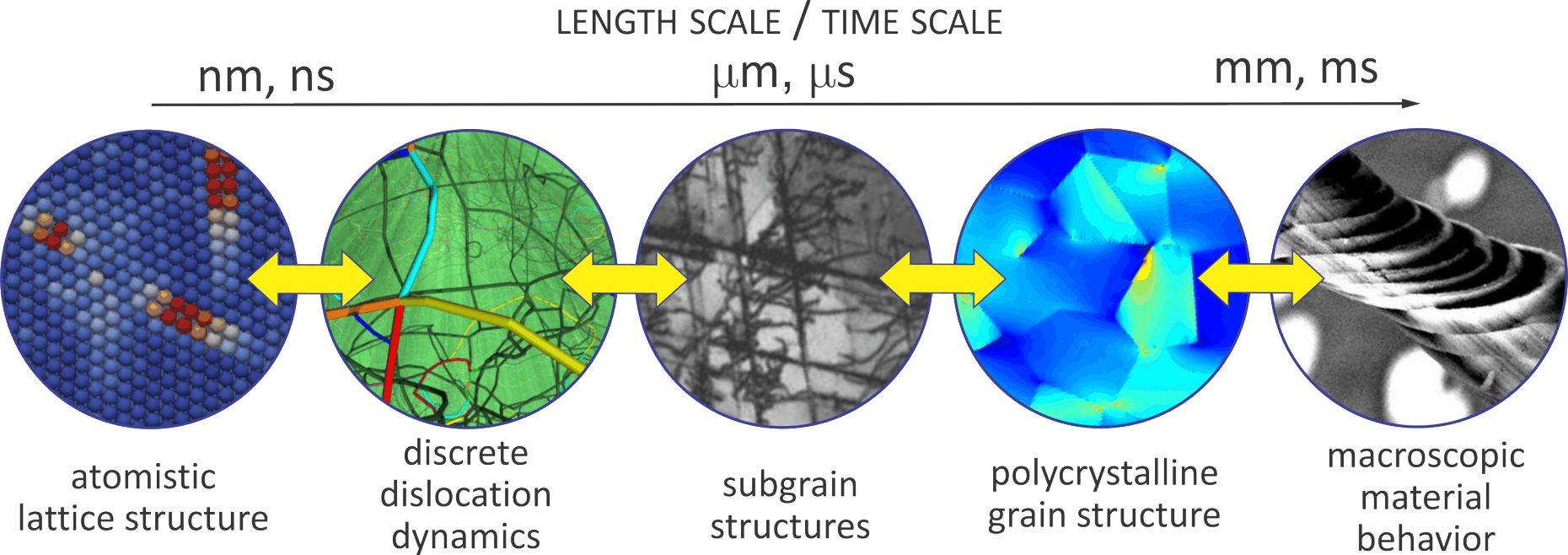
Course Contents
- Review of continuum and computational mechanics
- Separation of scales, representative unit cell, types of microstructures
- Homogenization theory, averaging theorems, micro-to-macro transition
- Spectral methods, Bloch wave analysis
- Cauchy-Born assumption, analytical homogenization methods
- Relaxation theories, multiscale constitutive models.
- Atomistics, molecular statics and dynamics, brief intro to statistical mechanics
- Discrete-to-continuum coupling techniques, coarse-grained atomistics, quasicontinuum techniques,
- Connecting quantum mechanics, atomistics, mesoscale and macroscale