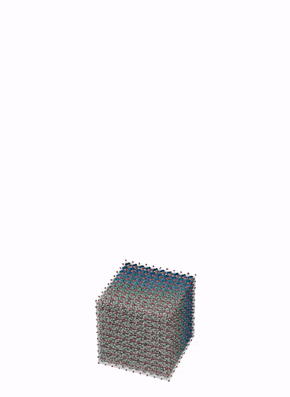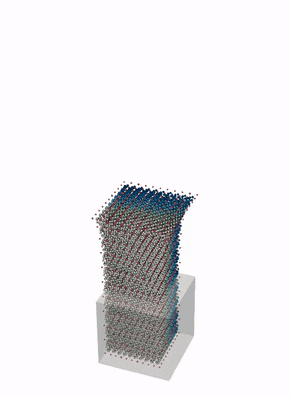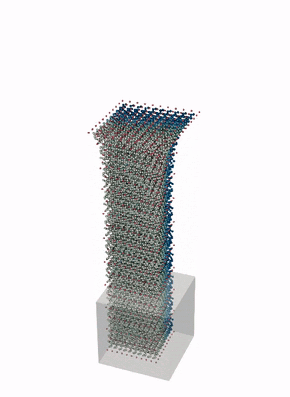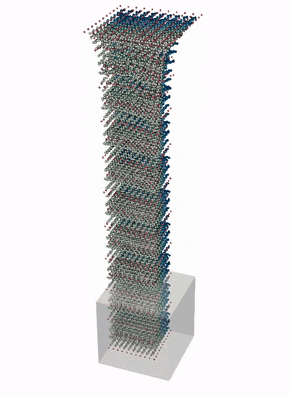Meshless Modeling
The finite element method (FEM) has been widely successful in simulating the mechanics and physics of solids. Unfortunately, conventional FEM is often severely limited when solving problems involving complex geometries and, especially, large deformations. In this latter context, problems associated with classical FEM are two-fold. First, formulating the governing equations in the initial or reference configuration (referred to as total-Lagrangian description) often becomes inapplicable in case of large deformations, where the initial mesh loses relevance. Second, when formulated in the updated-Lagrangian or Eulerian settings, severe mesh distortion may lead to entangled or ill-shaped elements. We develop meshless methods which, in contrast to mesh-based methods, are more suited for simulations involving large deformations and distortions, and circumvent mesh-related problems by treating nodes as interacting particles. We apply these methods to study a range of multiscale and multiphysics problems – from thermomechanical processing of metals to coarse-grained atomistics.
Despite their advantages, conventional meshless methods have historically suffered from tensile instability in an updated-Lagrangian setting, which greatly limits their potential in simulating large-deformation mechanics. To this end, we introduced an external page enhanced meshless scheme, which is based on the local maximum-entropy strategy as a compromise between shape function locality and entropy in an information-theoretical sense. Our improved version is specifically designed for severe, finite deformation and offers significantly enhanced stability as opposed to existing meshless methods. This is achieved by (i) formulating the quasistatic mechanical boundary value problem in a suitable updated-Lagrangian setting, (ii) introducing anisotropy in the shape function support to accommodate directional variations in nodal spacing with increasing deformation and eliminate tensile instability, (iii) spatially bounding and evolving shape function support to restrict the domain of influence and increase efficiency, (iv) truncating shape functions at interfaces in order to stably represent multi-component systems like composites or polycrystals.
The below animations illustrate applications of this scheme to the deformation of blocks of rubbery material (modeled as a hyperelastic solid).
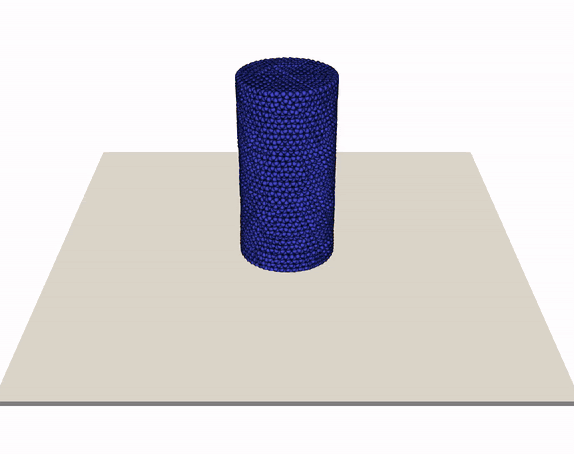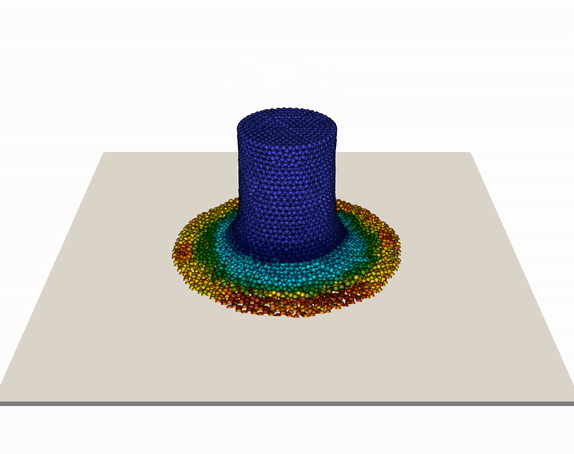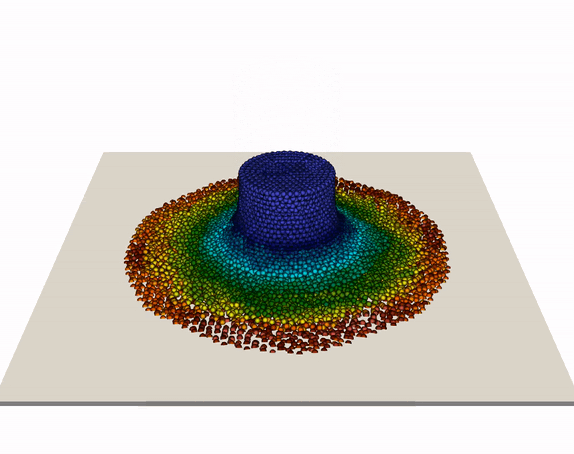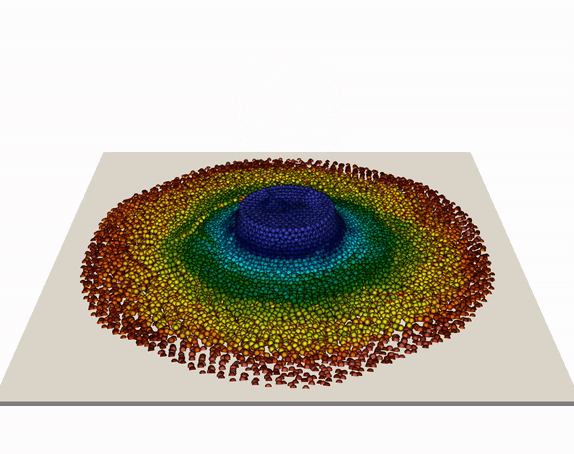
The so-called Taylor-anvil test (shown below) is a further benchmark case for our meshless modeling framework, which has been studied well in the literature and allows for quantitative assessment of the accuracy of our simluation toolset. An elastoplatic metal cylinder is simulated to hit a rigid wall at high velocity, resulting in (based on velocity and material) plastic deformation, fragmentation, failure, and more. Our animations illustrates a cylinder (modeled by von Mises plasticity with linear isotropic hardening) hitting a frictionless rigid wall. We simulated various initial speeds from 200 to 800 m/s, see external page our publication for details. Results compared well with experimental and numerical literature values for this scenario.
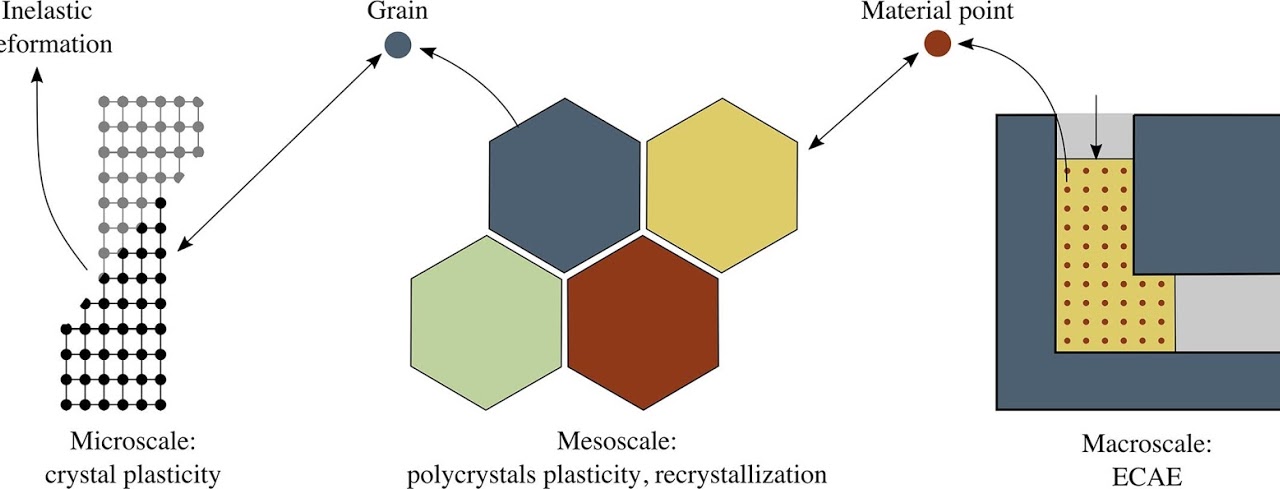
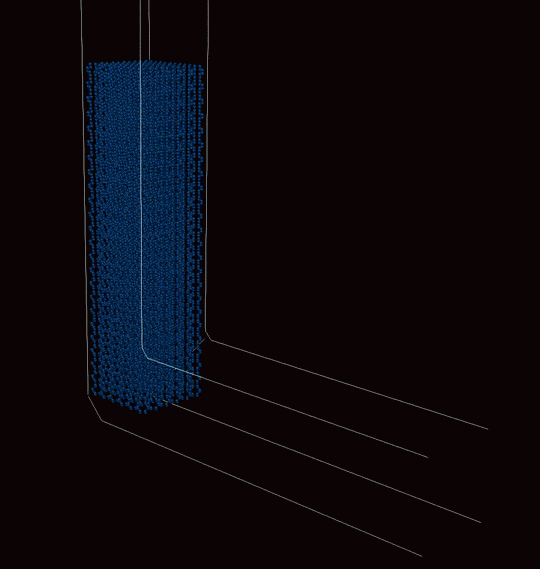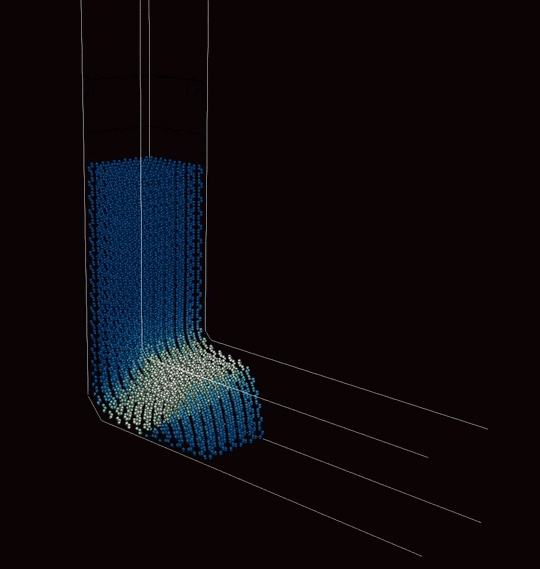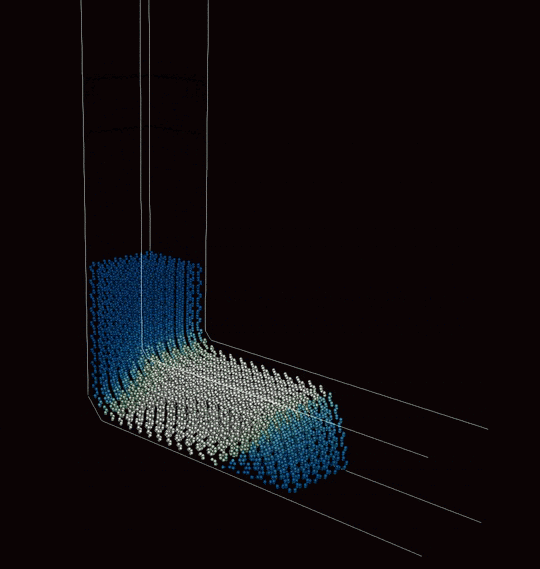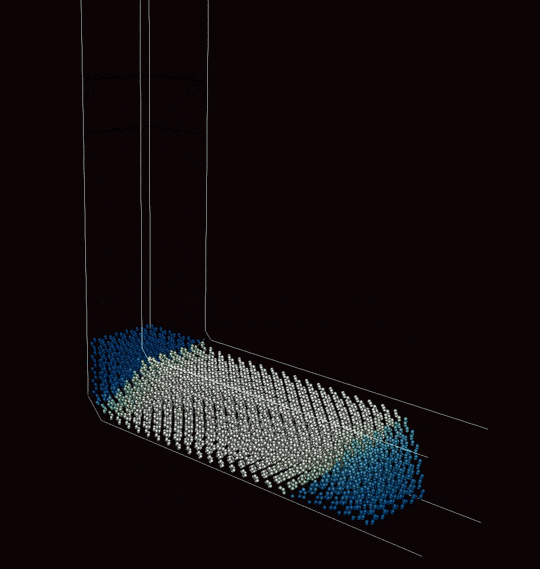
Our method can be integrated into a multiscale framework, which we demonstrated through a novel external page meshless multiscale approach to modeling severe plastic deformation of metals. Thermomechanical processes, e.g., equal-channel angular extrusion (ECAE), are ubiquitous across metal forming for improving bulk material properties such as the strength of metals. The latter is achieved by ultra-fine grain refinement at the polycrystalline mesoscale via the application of large plastic strains on the macroscale. The proposed multiscale framework aims at efficiently modeling SPD processes while effectively capturing the underlying physics across all relevant scales. At the level of the macroscale boundary value problem, the aforementioned enhanced maximum-entropy meshless method is employed, which offers a beneficial and stabilized finite-strain updated-Lagrangian setting for improved robustness with respect to mesh distortion arising from large plastic strains. At each material point on the macroscale, we describe the polycrystalline material response via a Taylor model at the mesoscale, which captures discontinuous dynamic recrystallization through the nucleation and growth/shrinkage of grains. Each grain in turn is modeled by a finite-strain crystal plasticity model at the microscale. Our framework describes not only the evolution of strain and stress distributions during the process but also grain refinement and texture evolution, while offering a computationally feasible treatment of the macroscale mechanical boundary value problem. Shown below are example applications for copper.
Going beyond (below) the microscale, we develop a novel external page meshless quasicontinuum (QC) method for scale-bridging from the atomistic to the continuum level. In this meshless framework, the finite element interpolation of conventional QC methods is replaced by nonlocal shape functions based on a local maximum-entropy strategy, which allows for improved adaptation functionality and coarse-graining in atomistic simulations (but also comes with increased computational expenses). In-depth details of our recent and on-going efforts on QC modeling (including and beyond the meshless approach) are available here.
Overall, we have a suite of versatile meshless techniques for applications in multiscale settings from continuum to atomistic levels (all developed and implemented in in-house C++ libraries), which are continuously extended to even more complex conditions and applied to a variety of technological and scientific applications.