Machine Learning

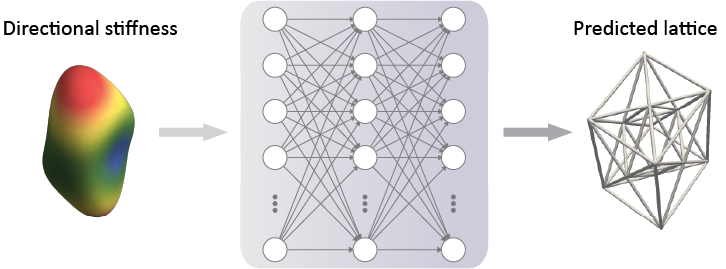
We leverage ML algorithms to tackle challenging questions in the context of computational mechanics and metamaterials. One of such problems is the inverse design of metamaterials: how does one efficiently identify a metamaterial design that exhibits given target properties? While traditional methods such as FEM are very successful in solving the forward problem – that is, identifying the mechanical properties of a given microstructural deisgn – they typically cannot be used efficiently for the inverse problem. Topology optimization, e.g., is a popular and successful inverse tool, yet it comes with significant computational expenses for large systems and high resolution. This is where ML comes into play. We have shown that certain NN architectures can successfully learn this inverse map, which has enabled the design of lightweight structures with spatially varying, locally optimized properties (such as the anisotropic stiffness), for applications from wave guiding to artificial bone.

Deep Learning for Inverse Design (Trusses)

Breakthroughs in additive manufacturing have established periodic trusses as a popular choice for creating metamaterials with tailored properties and functionality, required e.g., for topology optimization or wave dispersion. This success is mainly due to the freedom to freely tune the underlying unit cell (UC) architecture (i.e., its topology and geometry), which determines the macroscopic behavior of the truss. While effective properties such as the stiffness of a given truss lattice can be efficiently computed with the finite element method (FEM), the inverse problem – i.e., the identification of a UC best matching a desired homogenized stiffness among the uncountable many options, cannot efficiently be solved with the same techniques.

We use a data-driven inverse model based on a combination of neural networks (NNs) with enforced physical constraints to bypass this challenge. To obtain a large dataset of UC candidates, we generated millions of different UC architectures and pre-computed their corresponding homogenized constitutive tensors. Notably, the generated UC architectures differ both in qualitative and quantitative features (i.e., in their topology and geometry) to cover a large class of anisotropic mechanical responses. Once trained, results show that our inverse model accurately identifies UC architectures matching previously unseen stiffness responses, while also being orders of magnitude more efficient than traditional optimization frameworks such as FEM. More importantly, this does not only hold for queried stiffnesses from our precomputed database but also for more distant examples taken from the literature such as experimentally measured bone specimens (which is of interest for synthetic bone implants). We can furthermore extend the generative ability of our inverse model by introducing a stochastic sampling for all suitable topologies, such that different UCs (all closely matching the given stiffness response) are proposed – effectively giving the designer more freedom in choosing the appropriate UC.

Lastly, we presented a strategy to smoothly grade between any predicted UCs (each locally matching a given stiffness), without encountering dangling beams or other issues typically arising in the spatial grading of quasi-periodic structures. Functionally graded macrostructures can thus directly be generated by spatially grading the inversely designed UCs on the microscale, and optimized, e.g., for the response to loads (such as in multiscale topology optimization) or, by locally tailoring wave motion by lattice topology, for wave guidance and acoustic cloaking, which constitutes upcoming directions of research.

Deep Learning for Inverse Design (Spinodoids)

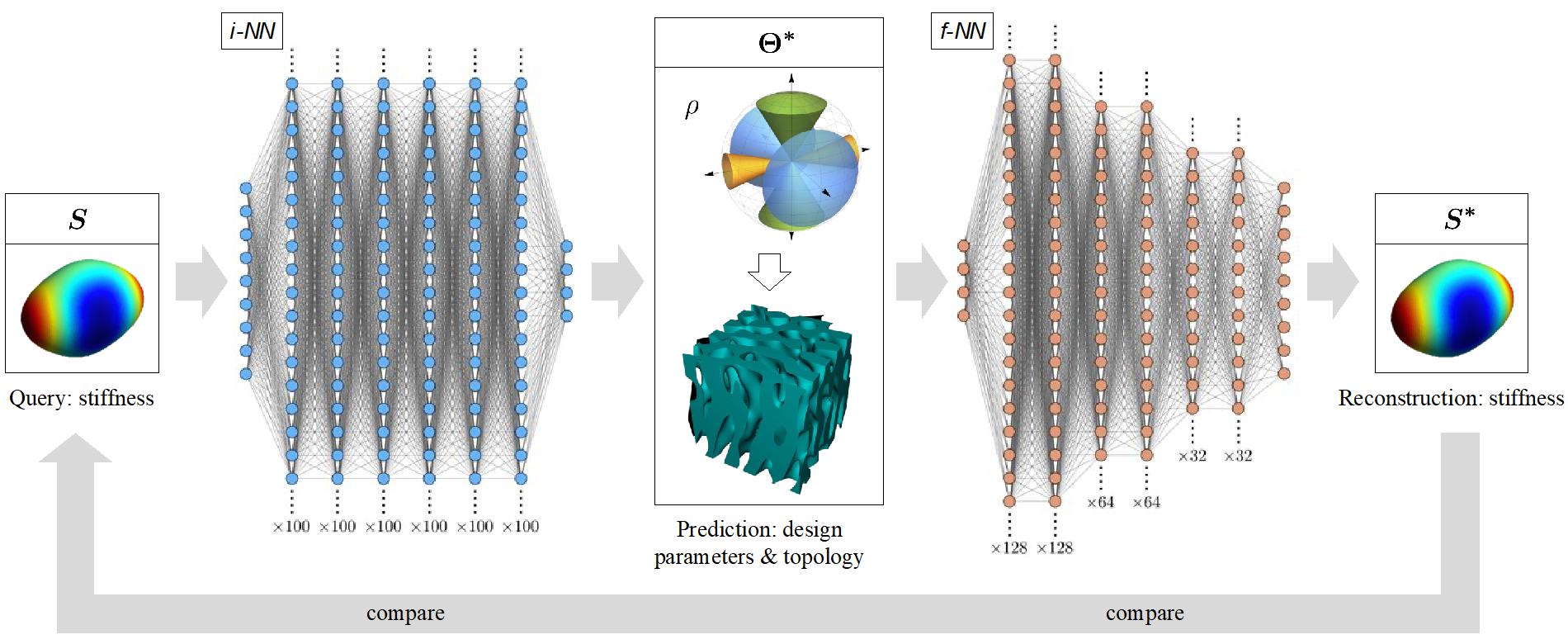
Inspired by natural self-assembly processes, spinodoid metamaterials are a close approximation of microstructures observed during spinodal phase separation. Their theoretical parametrization is so intriguingly simple that one can bypass costly phase-field simulations and obtain a rich and seamlessly tunable property space. Counter-intuitively, breaking with the periodicity of classical metamaterials is the enabling factor to the large property space and the ability to introduce seamless functional grading. We have introduced an efficient and robust ML technique for the inverse design of (meta-)materials which, when applied to spinodoid topologies, generates uniform or functionally graded cellular mechanical metamaterials with tailored direction-dependent (anisotropic) stiffness and mass density (fill fraction). Our data-driven approach is based on the integration of two neural networks for the forward and inverse problems. This approach provides a computationally inexpensive two-way relationship between design parameters and mechanical properties. We apply this framework to generate spinodoid metamaterials with as-designed anisotropic elastic stiffness.

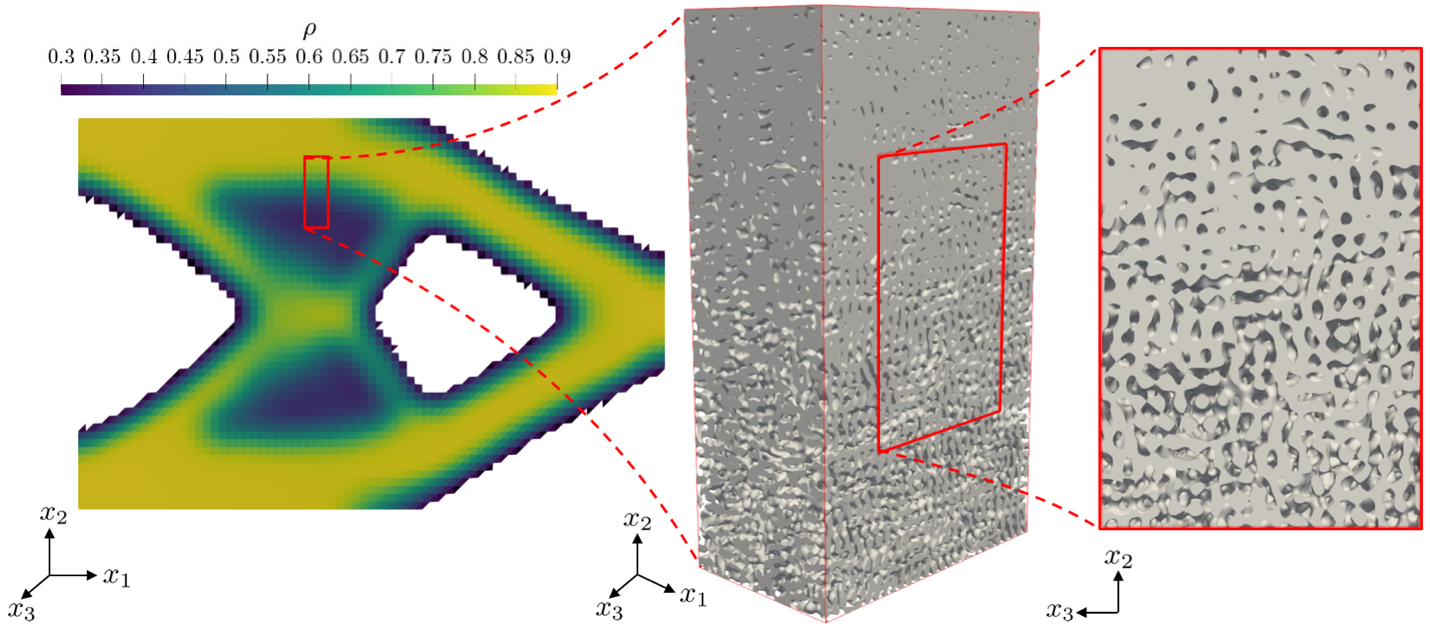
The forward map of the structure-property relation can also be integrated into multiscale topology optimization to accelerate the design process of (meta-)materials with a wide range of tunable mechanical responses. We have introduced a two-scale topology optimization framework for the design of macroscopic bodies with an optimized elastic response, which is achieved by means of a spatially-variant cellular architecture on the microscale. The chosen spinodoid topology for the cellular network on the microscale admits a seamless spatial grading as well as tunable elastic anisotropy, and it is parametrized by a small set of design parameters associated with the underlying Gaussian random field. The macroscale boundary value problem is discretized by finite elements, which in addition to the displacement field continuously interpolate the microscale design parameters. By assuming a separation of scales, the local constitutive behavior on the macroscale is identified as the homogenized elastic response of the microstructure based on the local design parameters. As a departure from classical FE²-type approaches, we replace the costly microscale homogenization by a data-driven surrogate model, using deep neural networks, which accurately and efficiently maps design parameters onto the effective elasticity tensor. The model is trained on homogenized stiffness data obtained from numerical homogenization via finite elements. As an added benefit, the machine learning setup admits automatic differentiation, so that sensitivities (required for the optimization problem) can be computed exactly and without the need for numerical derivatives – a strategy that holds promise far beyond the elastic stiffness. Therefore, this framework presents a new opportunity for multiscale topology optimization based on data-driven surrogate models.

Further areas of research include the application of graph neural networks to obtain surrogate models for beam lattices. As the latter can conceptually also be interpreted as a graph (where beams and their intersections can be understood as its edges and nodes), these frameworks might prove highly capable to capture the mechanical behavior of such structures. Another ongoing research direction is the application of the recently introduced physics-informed neural networks (PINNs) to solve and optimize physical systems governed by partial differential equations (PDEs) in the context of computational mechanics. Contrary to the previous frameworks, these algorithms learn the physical relations in an unsupervised manner, i.e., they do not rely on a pre-computed catalog of training data. Instead, they are trained by directly enforcing the outputs of the PINN to fulfill the governing equations. One advantage of these methods compared to classical numerical methods is their straightforward extension to optimization or inference problems, since the loss function for these networks can be extended to account for secondary objectives such as minimizing the compliance of the structure – and we thus try to solve the underlying physical equations while simultaneously optimizing for the structure with the highest stiffness.

Graph Neural Networks for Truss Structures

Beam networks can be naturally described as graphs, whose edges and nodes represent beams and their intersections. The connectivity or topology of these networks largely determines their mechanical properties. We leverage Graph Neural Networks (GNNs) within architectures such as the Variational Autoencoder to tackle both the property prediction as well as the inverse design of these systems. For instance, given the target elasticity of a lattice-based material, we infer families of topologies that give rise to that desired effective property. The design outcome is evaluated not only on the basis of achieving that mechanical property but also on the novelty and validity (manufacturability) of the generated architecture.

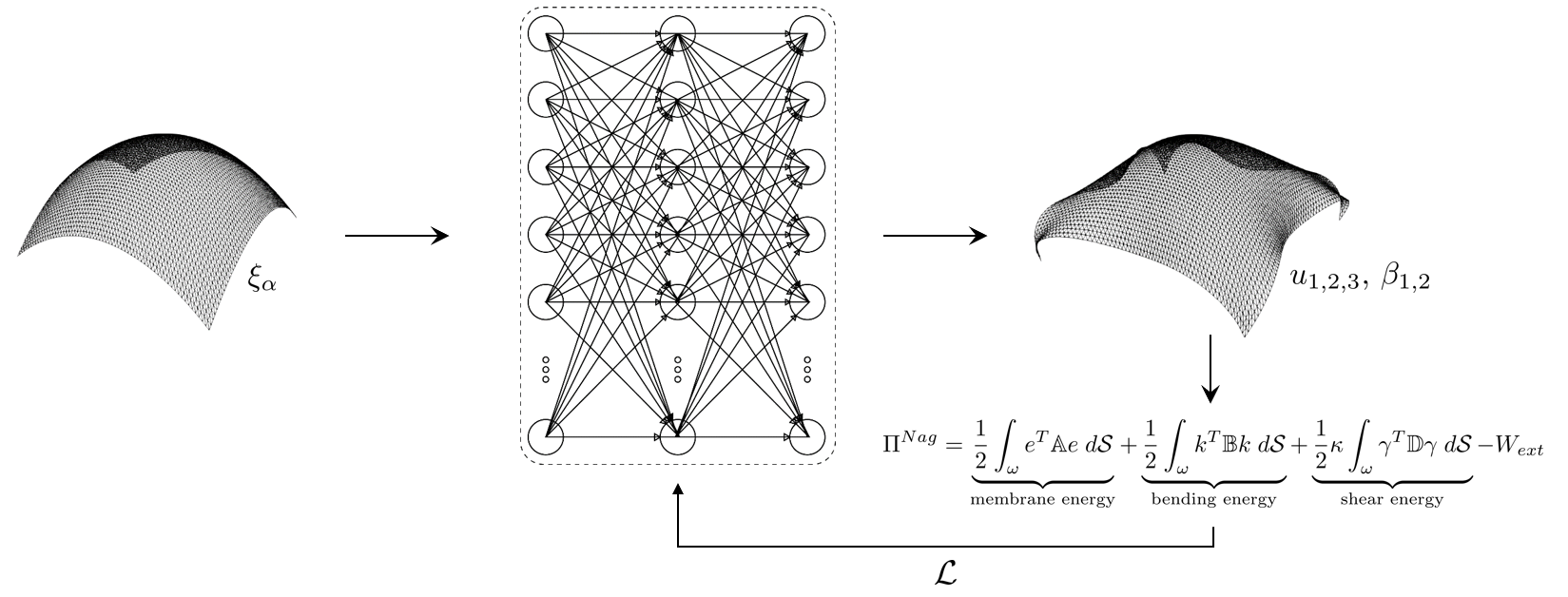
PINNs for Shell Theory

While physics-informed neural networks (PINNs) were proposed several decades ago, they have gained momentum only recently due to their straightforward and efficient implementation in modern ML libraries and demonstrated empirical success in solving systems described by PDEs. The key idea is simple: as the governing strong or weak form of many physical systems is often well-known, we encode it within the loss function used to train a NN. This PINN then maps from a finite set of collocation points in the given domain to the unknown function, from which the loss function can be constructed. Typically, the loss function is taken as the deviation of the predicted output from the given strong from (i.e., the physical PDE), such that the underlying NN is trained to fulfill the strong form at every given collocation point. If trained successfully, it indeed has learned the physical response of the system, without relying on any pre-computed data. Although PINNs cannot fully compete with classical methods such as FEM in terms of computational efficiency and theoretical underpinning yet, they offer a variety of advantages and potential. In our lab, we currently investigate the application of PINNs to the theory of shells, which, although being among the most common structures found in nature and society, are notoriously challenging to solve with FEM.