Truss Metamaterials

Redefining the mechanical property space of architected materials

The mechanical behavior of architected solids is of enormous interest, owing to the extreme level of tunability that admits the creation of novel materials with optimal elastic and inelastic properties. We have investigated a long list of interesting aspects of truss metamaterial deformation mechanisms, including elastic and inelastic properties (stiffness, strength, toughness, etc.) as well as wave propagation and attenuation.

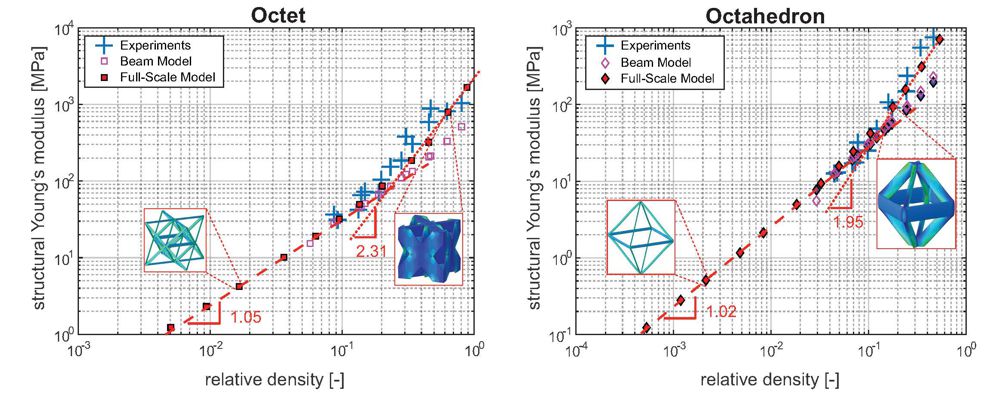
Especially at small scales, size effects may play an important role. Through collaborations with external page Prof. Julia R. Greer and team at Caltech, we have investigated the performance of nanolattices, in which intrinsic size effects arise from the material's microstructure and, e.g., show that a base material's strength increases with decreasing average grain size, thus demonstrating a smaller is stronger behavior. This phenomenon is reversed at small grain sizes on the nanoscale near 20 nm, below which the behavior transforms into smaller is weaker. In contrast, extrinsic size effects are observed in small-scale structures and arise from the abundance of free surfaces and the small volumes in nanoscale structural members. Here, strength increases with decreasing feature size of single-crystalline samples (smaller is stronger) due to dislocation starvation and the attraction of existing defects to free surfaces. In polycrystalline samples, size effects and their underlying mechanisms are much more complex due to the interplay between competing effects arising from the characteristic microstructural sizes (e.g., grain size) and the characteristic structural feature sizes (e.g., truss diameter and wall thickness). This competition results in interesting size effects to be proliferated to the macroscale.

We have further investigated the scaling of stiffness and strength with truss architecture, exploring the extremely wide property space of solid and hollow periodic truss lattices. Besides the base material, the topology and geometry play an important role and - again - size effects may arise at the nanoscale (e.g., fabrication constraints lead to stubby beams, for which the classical scaling laws based on the slender-beam assumption no longer apply).

Reduced-order modeling of hierarchical truss networks

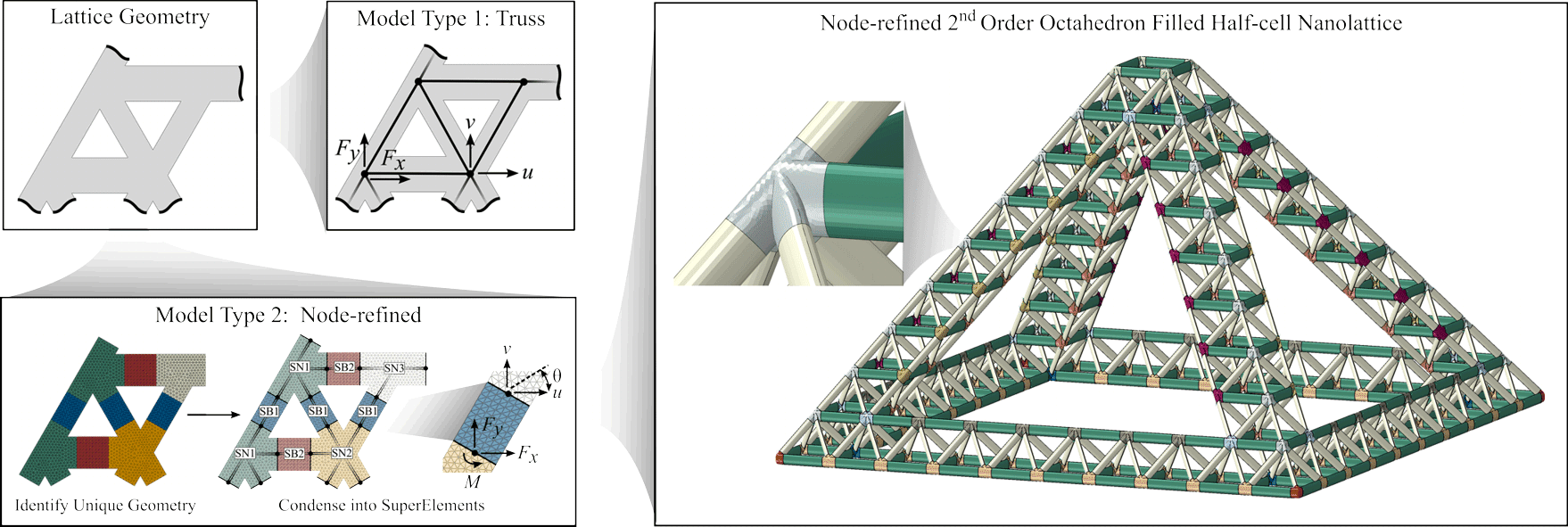
When considering the elastic nanotruss behavior up to plastic yielding, we showed that methods of continuum mechanics are indeed appropriate to predict the effective structural response. In collaboration with the group of external page Prof. Julia Greer, we studied the mechanics of hierarchical lattice networks, which are commonly found in biomaterials such as bone and wood. Hierarchical structures are hypothesized to be robust and damage-tolerant due to their scale-spanning architecture, but they are exceedingly difficult to model since they can have length scales spanning many orders of magnitude and they may require the representation of thousands to millions of truss members. We used the finite element method and introduced reduced-order models of solid, hollow, and composite hierarchical nanolattices by kinematically constraining the deformation of fully-resolved lattice beams and nodes (as shown below). By condensing the degrees of freedom from the kinematic constraints, we created a simplified model that accurately matches the linear elastic behavior of a variety of hierarchical nanolattices fabricated and tested experimentally.

One of the significant drawbacks of these truss structures is the immense computational expense required to predict the mechanical response of the large amount of individual truss members. Understanding the effective response of such truss metamaterials calls for efficient modeling techniques that further enable us to improve, optimize and design the response of architected materials through an inverse-design strategy. As the costs of simulating the response of small-scale truss networks by classical tools such as the finite element method is rapidly growing with larg truss networks containing thousands, millions and more of individual struts, advanced and efficient approximations are required.

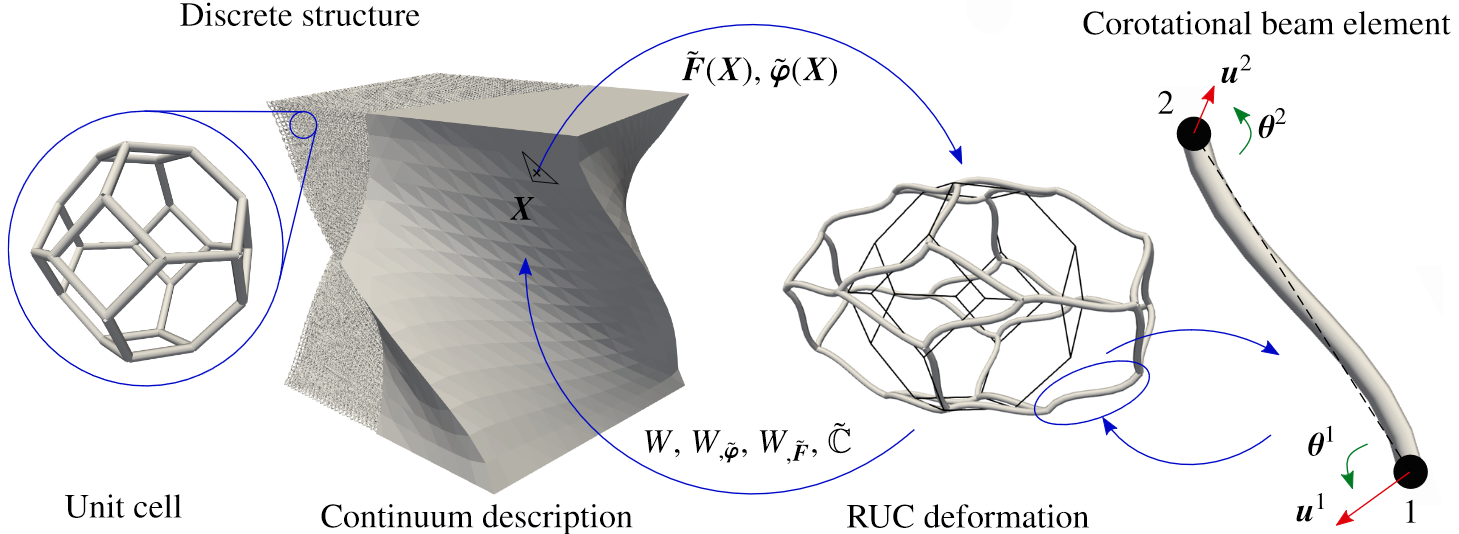
Among others, we introduced a continuum description of 2D and 3D truss lattices based on the (non-)local Cauchy-Born rule, that allows us to bridge between a microscopic representative unit cell and a macroscopic boundary value problem. Separation of scales gives us the capability of accurately representing a large underlying periodic discrete lattice while requiring only a fraction of the degrees of freedom in a finite element simulation. Our model considers translational and rotational degrees of freedom to describe general nonlinear beam bending, resulting in a higher-order continuum theory on the macroscale. Unlike related Cosserat or micropolar theories, we do not postulate any effective energy density or constitutive model on the continuum scale, but we compute the effective response on the fly from a representative unit cell. On the microscale, we use a multi-lattice approach for stretching- and bending-dominated truss lattices and show that the decomposition into multiple superimposed Bravais lattices with relative shifts in between leads to improved performance of the continuum model and a more accurate representation of the mechanics of bending-dominated truss structures. Besides developing the underlying theory, we develop numerical tools to deploy the new techniques in engineering problems.  

We demonstrated the capabilities of our continuum approach by a set of numerical examples undergoing significant, nonlinear stretching, bending, and torsional deformation (external page IJSS 2020). The generalized continuum description shows good agreement with discrete simulations while incurring only a fraction of the computational costs. We show that the model also applies for large deformation when structural instability and localizations dominate the macroscopic response (as long as the representative unit cell is appropriately chosen). We have also extended the approach to arbitrarily-shaped trusses on the macroscale (see the example below).

Quasicontinuum method for periodic 3D trusses

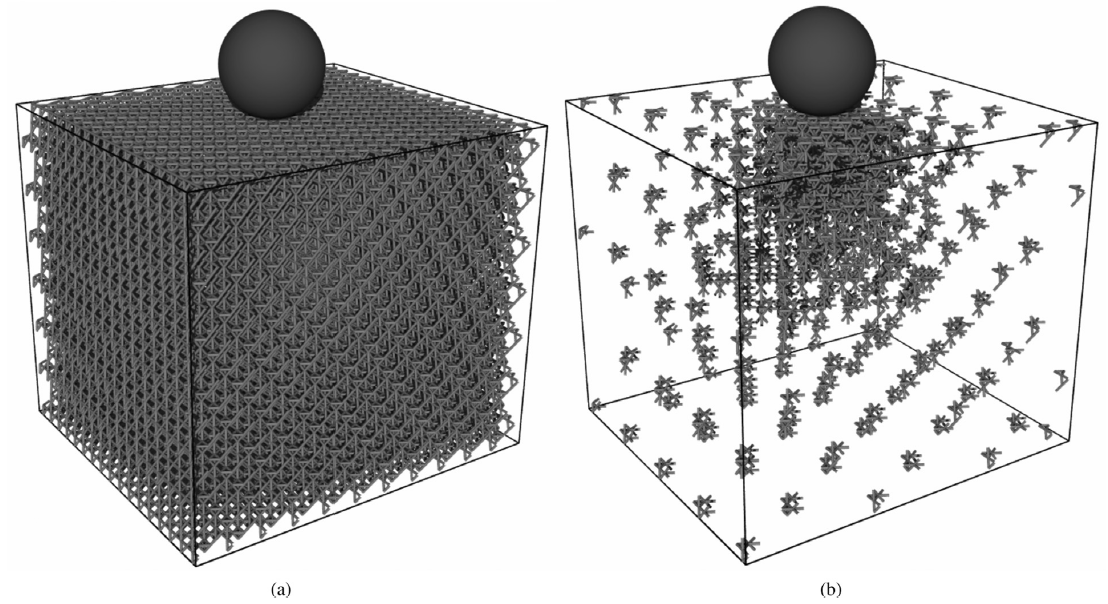
In order to understand the fundamental deformation and failure mechanisms in nanoscale metallic solids, we have used the external page quasicontinuum (QC) method to simulate their mechanical behavior. The original QC method bridges across scales from atomistics to the continuum and enables to extend local atomistic accuracy to larger scales by providing finite-element efficiency. Here, we extended the classical, atomistic QC method to 3D trusses that undergo nonlinear elastic or inelastic bending, stretching and torsion. We account for elastic beam behavior (including finite rotations), plasticity and failure. Shown below is the simulated response of a 3D truss impacted by a rigid circular object.

As in the classical QC technique for atomistics, the goal is to reduce full resolution to regions of interest while coarsening the remaining simulation domain into a continuum framework to gain efficiency. Shown below are simulation snapshots of the fully-resolved 3D truss before impact as well as of the same truss represented by the efficient QC model (shown are only all those truss junctions that are in fact taken into account, leading to a significantly reduced total number of degrees of freedom).

Selected ongoing research projects:

• We predict the viscoelastic response of truss metamaterials via a generalized continuum approach. Including linear viscoelasticity in a corotational beam setup within the Cosserat-type truss continuum described above allows us to efficiently describe the time-dependent response of complex truss networks. This makes the approach appealing for applications from wave attenuation to impact mitigation.
  
• We study the influence of various types of imperfections on the mechanical response of truss metamaterials. Fabrication-induced imperfections in trusses such as deviations in nodal positions, variations in beam diameter, missing struts, or waviness of struts alter the effective response of the overall truss, which we study both numerically and experimentally to compare the imperfection sensitivity of 2D and 3D truss lattices. Through methods of machine learning we aim for an approximate predictive tool that links the amount and magnitude of imperfections to the resulting metamaterial response.
• See also our work on geometrically-exact discrete beam models.