Exploiting Instabilities
Metamaterials are synthetic, engineered materials and systems which often exhibit properties found beyond natural materials (including extreme or counterintuitive physical behavior). Current research in the field of mechanical metamaterials is primarily focused on the enhancement of quasistatic properties such as strength, stiffness, and reconfigurability, under either conservative (free of energy dissipation) and/or linear (small-amplitude waves) assumptions. Applications range from acoustic lenses and diodes, sound and vibration isolators, acoustic sensors and cloaks, to energy absorbers and sonar stealth technologies. In contrast, research in nonlinear metamaterials made of periodic building blocks that undergo large deformation and possibly structural instability is still in its early stages.
In recent years, we investigated nonlinear mechanical metamaterials, which, unlike linear systems, permit multiple types of wave solutions and thus can be tuned to propagate a variety of waves having small or finite amplitudes with potential applications in soft robotics, mechanical logics, energy storages, and deployable space structures. With our collaborators Professors Chiara Daraio, Katia Bertoldi, Jennifer Lewis, and Jordan Raney, we have explored strategies to design such nonlinear systems, analyzed their performance theoretically, fabricated prototypes, and characterized their dynamic behavior experimentally.
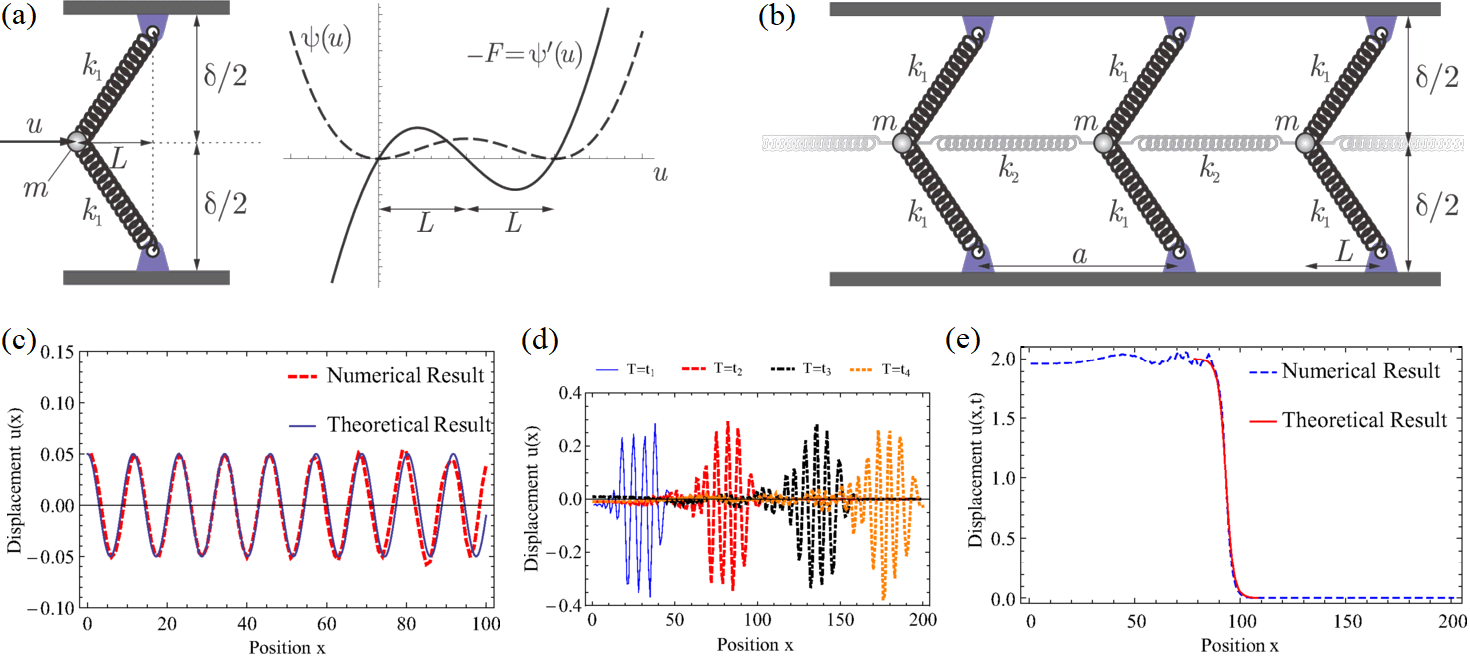
Consider, e.g., the grounded periodic elastic chain shown below, in which structural buckling and snapping leads to large nonlinear motion. The dynamics of this structure display four independent regimes of wave propagation, linear, weakly nonlinear, strongly nonlinear, and pre-compressed strongly nonlinear waves. For each regime, we have derived external page analytical solutions for the propagating wave and have characterized the wave profiles and speeds. At small amplitudes, linear acoustic waves travel through the structure, whose dispersion relation can be controlled by the amount of precompression applied to the system. At moderate amplitudes, envelope solitary waves transport localized energy packages through the array. At large amplitudes, a transition wave propagates down the chain by subsequently snapping each element (here, precompression can be utilized to not only alter the wave speed but also, in the presence of damping, to force the wave propagation to be unidirectional, resulting in nonlinear mechanical diodes).
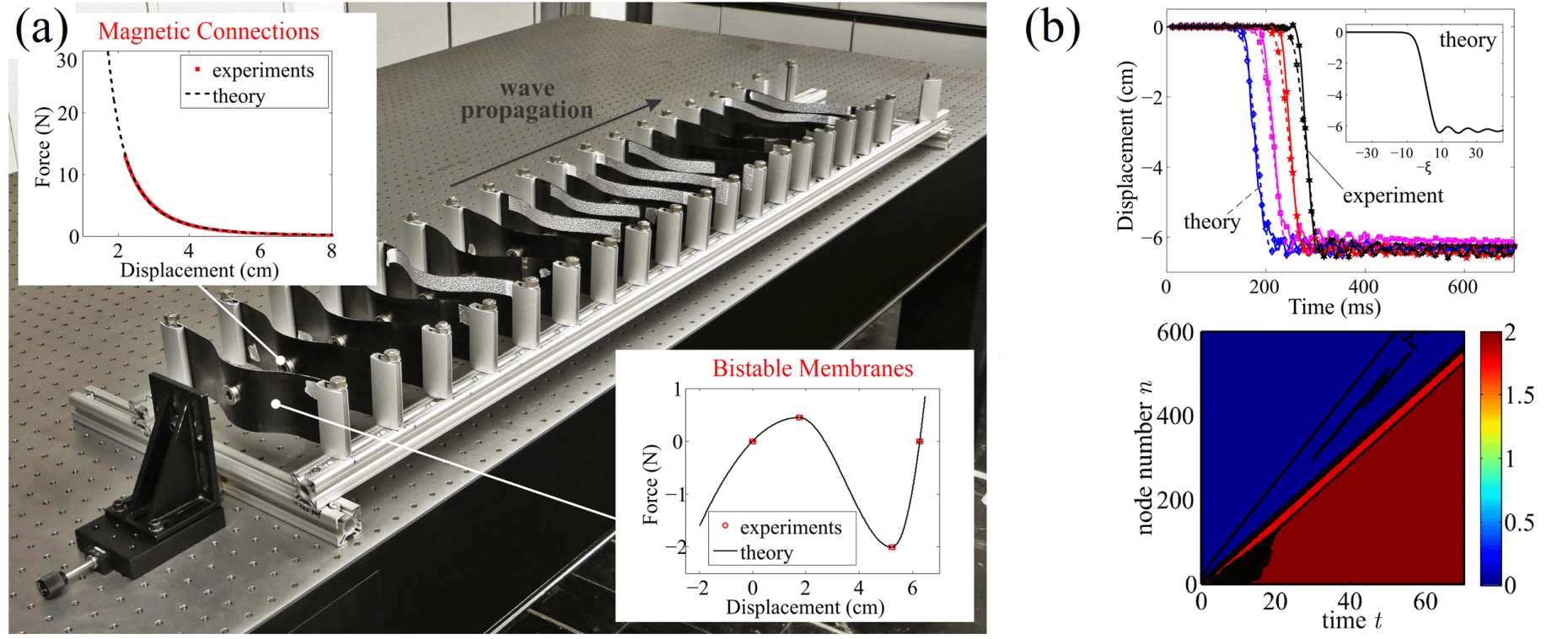
Most interesting is the strongly-nonlinear transition wave whose energetics were further investigated theoretically. We derived a external page universal scaling law that shows how the speed of the propagating transition front is related to the difference in energy of the two stable equilibrium configurations, the damping in the system, and the shape of the propagating kink. Interestingly, in this case, scaling law is linear despite the highly nonlinear nature of the problem. Also, it is unaffected by the interactions between bistable elements and holds in the case of vanishing masses (diffusive/dissipative system). To test our theory, we built a external page macroscopic structure consisting of bistable membranes elastically connected by repelling permanent magnets, which is shown below. The fabrication method renders the composite membranes inherently asymmetric, resulting in a non-symmetric energy potential (i.e., one equilibrium has higher energy than the other). As a consequence, we observed stable transition waves of constant propagation speed that propagate only unidirectionally, thus displaying the behavior of a mechanical diode. We note that despite the complex three-dimensional motion of the snapping membranes, the wave propagation can be described accurately by a one-dimensional model.
Demonstrations of transition waves in multistable structures:
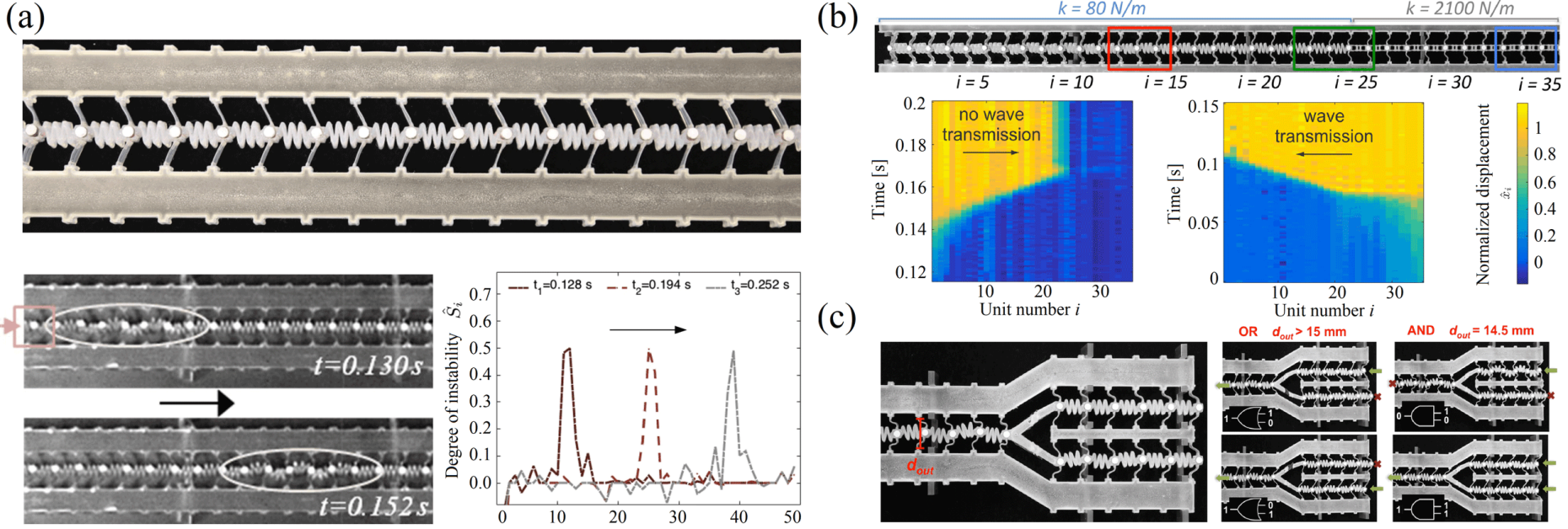
Our experimental collaborators have also fabricated a external page smaller-scale bistable chain shown above, using state-of-the-art 3D printing techniques. This system, made of polymeric materials, has high internal damping so that linear waves are attenuated almost instantaneously. By contrast, transition waves propagate at a constant speed over, in principle, infinite distances. The speed of the kink arises from the balance between energy release due to snapping and energy absorption due to damping. Again, the diodic motion was apparent, and we used the same building principle to build elements of mechanical logic such as switches and diodes, as well as for wave tuning (e.g., to control the wave speed). Shown below are example systems.
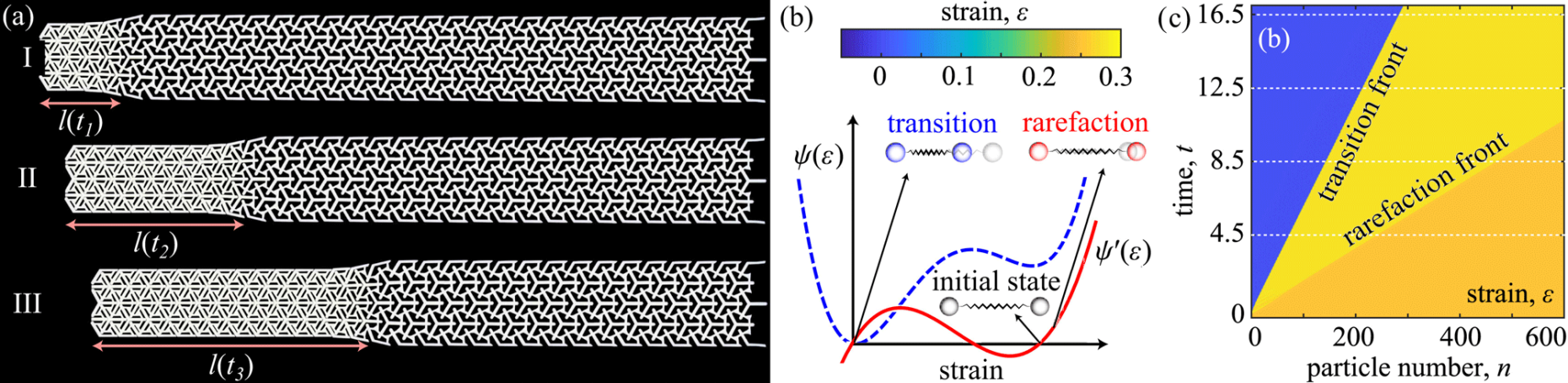
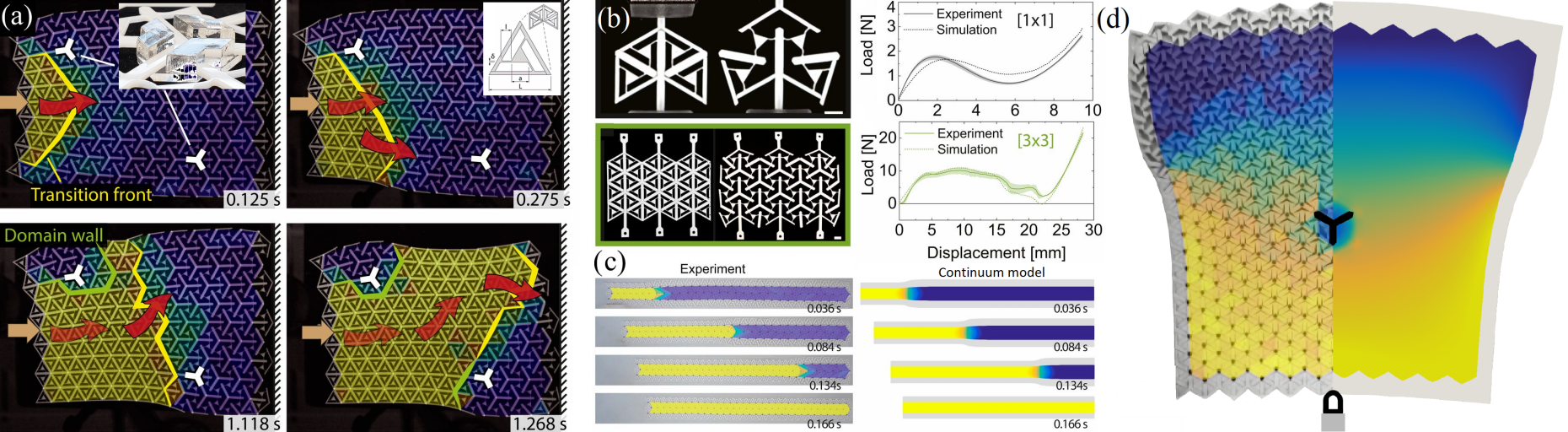
Contrasting the grounded systems, we have also studied external page substrate-free dissipative metamaterials (analogs for solid-solid phase transformations), in which unit cells are only attached to their neighboring unit cells and not to a substrate. In these systems, the non-convex potential depends on the gradients of the primary fields of displacements, electric or magnetic fields. In these systems, generally, two propagating fronts coexist, and the system locally goes through an intermediate rarefaction state, thus producing both a rarefaction front (shock) and a transition front (kink). We derived solutions for the two fronts as well as the energy balance relation in the 1D chain, revealing the characteristics of the fronts are related to energetics, density, and damping of the system and unlike the grounded chains, inertia plays a central role through the kinetic energy of the moving system. The derived relations in both grounded and substrate-free studies apply to domain wall motion in a variety of physical, chemical, and biological systems, including, e.g., ferroelectric or ferromagnetic domain wall motion (the 1D theory also applies to wavefronts in higher dimensions).
Going to higher dimensions, increasing the size and complexity of these substrate-free reconfigurable makes the discrete description of them cumbersome and computationally expensive. Hence we developed a continuum description based on the concepts of homogenization to simulate transition waves in these structures efficiently. We examined the performance of this approach through several examples of metamaterials and structures made of bistable unit cells in 2D and 3D, which also serve to highlight the versatility and potential of the multistable design approach to achieving as-designed sequences of target motion. In fact, these metamaterials admit precise control of the transition direction, shape, and velocity through spatially tailoring the underlying periodic network architecture (locally varying the shape or stiffness of the fundamental building blocks, and exploiting interactions of transition fronts with lattice defects such as point defects and free surfaces). We used our continuum model to explore the design space of external page multistable metamaterials and showcased how defects can be used to guide transition waves in complex structures. We described 2D experiments in the absence and presence of defects, which was shown to redirect or pin transition waves, as well as to split, delay, or merge propagating wavefronts. This programmable strongly nonlinear metamaterial motion has potential applications in morphing surfaces, reconfigurable devices, mechanical logic, propulsion in soft robotics, and controlled energy absorption.